Wednesday, August 29, 2007
Catenoid-Helicoid vs Torus-Nanospring
Two most famous minimal surfaces are the catenoid and helicoid as shown by the figures from the Indiana university.


In fact, we have already created these two surfaces at the intermediate stages in weaving torus and nanospring. One can obtain these two kinds of minimal surfaces simply by throwing away all pentagons.
I don't have good examples to illustrate this point, hopefully, we can create some beaded models to demonstrate this. Here is a picture that I tried to show how to make T120. Interestingly, in the intermediate stage, I have a catenoid.


In fact, we have already created these two surfaces at the intermediate stages in weaving torus and nanospring. One can obtain these two kinds of minimal surfaces simply by throwing away all pentagons.
I don't have good examples to illustrate this point, hopefully, we can create some beaded models to demonstrate this. Here is a picture that I tried to show how to make T120. Interestingly, in the intermediate stage, I have a catenoid.
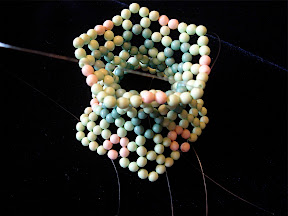 |
Tuesday, August 28, 2007
Schwarz H Surface
The minimal surfaces at the Indiana university has a beautiful Minimal Surface Archive. Here are two pictures of Schwarz' H-surface I found in that site:


Believe it or not. Chuang Chern has constructed a beaded model for this IPMS. I will ask him to post it later. It is now natural to ask whether all IPMS can be tiled by graphene sheets or not.


Believe it or not. Chuang Chern has constructed a beaded model for this IPMS. I will ask him to post it later. It is now natural to ask whether all IPMS can be tiled by graphene sheets or not.
Saturday, August 25, 2007
Google sketchup for molecular modeling?
I checked the google 3D warehouse and found many interesting models including domes, polyhedrons, buckyballs. I am wondering the possibility of creating either the arbitrary sp2 carbon structures or more challangingly the beaded models with the google sketchup, which seems to be a very good free software for the 3D CAD.
The figure below shows a few sample objects I found from the 3D warehouse.

Personally, I found the polyhedral dome in the upper right corner interesting. It would be interesting if we can build toroidal-shaped dome. Additionally, the google sketchup seems to provide the best free software for us to play with the idea of public arts.
The figure below shows a few sample objects I found from the 3D warehouse.

Personally, I found the polyhedral dome in the upper right corner interesting. It would be interesting if we can build toroidal-shaped dome. Additionally, the google sketchup seems to provide the best free software for us to play with the idea of public arts.
Saturday, August 18, 2007
On weaving rules again
Previously, I suggested that there are essentially two kinds of rules in weaving a beaded model: local and global. Local rules consist of the description of tiles such as 5-, 6-, 7-, and 8-gons and the how to connect these polygons locally. For gyroidal graphenoid, the local rules are quite clear, but the global rules are harder. I have thought about what I meant by the global rules these two days. It seems to me that the global rule is something like the weaving codes I developed for small fullerenes. Somehow this is similar to the Hamiltonian chain that specify how the weaving procedure goes. Of course, it is easy for simple object like the simply-connected fullerenes. However, it becomes not so clear for gyroidal graphenoid. What is the simplest weaving path (the Hamiltonian chain) for this system. I don't think Hamiltonian chains exist in this system. (Maybe I am wrong) But in order to weave this system effectively, maybe we should have a better global rule.
Another way to handle this is to follow Chuang's recipe and weave many unit cells and patch them together. It may also be the best way to build gyroidal graphenoid since I have played with my local and global rules for several hours without success. Then we can simply forget what I say here.
Another way to handle this is to follow Chuang's recipe and weave many unit cells and patch them together. It may also be the best way to build gyroidal graphenoid since I have played with my local and global rules for several hours without success. Then we can simply forget what I say here.
Friday, August 17, 2007
On the weaving procedure for constructing a gyroidal graphnoid
After a careful examination of the arrangement of hexagons and octagons in Chuang's first model. I found a simple weaving procedure for the construction of a gyroidal graphenoid. This procedure consists of several rules for weavings:
Local rules:
1. Every hexagon is surrounded by six octagons. (see Fig. a)
2. Every octagons is surrounded by four hexagons and four octagons arranged in an alternant pattern.
(Since there are two types of CC bonds, 6-8 bonds and 8-8 bonds, so it is convenient to use two colors to represent these two different bonds)
Global rules:
3. ...? It is important. I only have a rough idea though. It is not very effective. Mistake can happen easily.
Global rules are hard to carry out. I spent several hours this morning. The resulting beaded gyroidal graphenoid is in fig. c. I have to confess that this beaded model is not particularly attracting.
The reason I'd like to find a geometry-independent weaving rules is that as long as we follow these rules, we can concentrate on weaving much more easily without paying attention to the 3D geometry information. Indeed in the weaving of the small fullerenes, I have found a general weaving rule based on the so-called spiral code.

Local rules:
1. Every hexagon is surrounded by six octagons. (see Fig. a)
2. Every octagons is surrounded by four hexagons and four octagons arranged in an alternant pattern.
(Since there are two types of CC bonds, 6-8 bonds and 8-8 bonds, so it is convenient to use two colors to represent these two different bonds)
Global rules:
3. ...? It is important. I only have a rough idea though. It is not very effective. Mistake can happen easily.
Global rules are hard to carry out. I spent several hours this morning. The resulting beaded gyroidal graphenoid is in fig. c. I have to confess that this beaded model is not particularly attracting.
The reason I'd like to find a geometry-independent weaving rules is that as long as we follow these rules, we can concentrate on weaving much more easily without paying attention to the 3D geometry information. Indeed in the weaving of the small fullerenes, I have found a general weaving rule based on the so-called spiral code.

The origin of monkey saddles in gyroidal graphenoid
For the simplest gyroidal graphenoid, the monkey saddle is created by six octagons that connected to the central phenyl group. Due to the strain among them, three octagon are pushed upward and connected to the phenyl group lying above; while the other three octagons are pushed downward and connected to the phenyl group below. This is similar to a three-layer cyclophane with three tethers connected each two of them.
For the next gyroidal graphenoid, the central phenyl is replaced by coronene, other structural features remain the same. Imagine now that we have instead of one unit cell, but an infinite number of them arranged at each lattice site. The geometric feature of this creature may easily be seen.
By the way, using this construct, the normal of each layer is along (111) direction. However, this is only one diagonal, there are three major diagonal in this system. The gyrodial graphenoid looks exactly the same along these three diagonals.I.e. threre are two other sets of monkey saddles lying on the layers whose normals are the other two diagonals.
For the next gyroidal graphenoid, the central phenyl is replaced by coronene, other structural features remain the same. Imagine now that we have instead of one unit cell, but an infinite number of them arranged at each lattice site. The geometric feature of this creature may easily be seen.
By the way, using this construct, the normal of each layer is along (111) direction. However, this is only one diagonal, there are three major diagonal in this system. The gyrodial graphenoid looks exactly the same along these three diagonals.I.e. threre are two other sets of monkey saddles lying on the layers whose normals are the other two diagonals.
Monkey Saddle
Just like what Chuang has said in previous comment, if we align the (111) direction of the gyroidal surface in one unit cell vertically and then view it from the side, it is easy to see that the whole structure of this unit cell exactly consists of three layer. The center of each layer is a monkey saddle.
I found something similar discussed in a paper by Klinowski (Exact computation of the triply periodic G minimal surface, CPL, 321, 363-371, 2000) in which the authors mentioned the so-called fundamental patches, the smallest portion of the surface from which the entire surface can be constructed. Similar concept can be found in the description of a crystal. Instead, here we have a patch of surface. Klinowski also pointed out in his paper that a unit cell of the G surface consists of 12 fundamental patches. I don't have Chuang's beaded model with me now. It would be interesting to check it.
I found something similar discussed in a paper by Klinowski (Exact computation of the triply periodic G minimal surface, CPL, 321, 363-371, 2000) in which the authors mentioned the so-called fundamental patches, the smallest portion of the surface from which the entire surface can be constructed. Similar concept can be found in the description of a crystal. Instead, here we have a patch of surface. Klinowski also pointed out in his paper that a unit cell of the G surface consists of 12 fundamental patches. I don't have Chuang's beaded model with me now. It would be interesting to check it.
Thursday, August 16, 2007
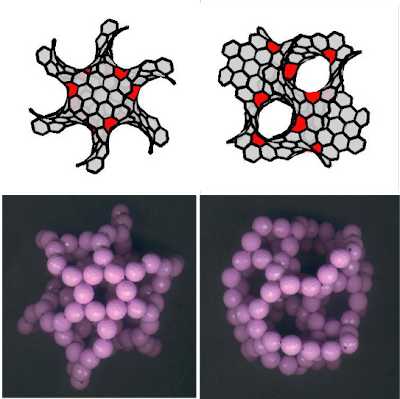
Smallest gyroidal graphenoid
Wednesday, August 15, 2007
IPMS and its beaded representation
IPMS ( Infinite Periodic Minimal Surfaces or Triply Periodic Minimal Surfaces) belong to an important class of surface forms. Among many family of these forms, the P-surfaces, the D-surfaces, and the gyroid surfaces are the most common structures that occur in nature. Previously, we have worked out the systematic tiling rules for the P- and D-surfaces. The beaded models for these two surfaces have also been constructed by Chuang.
But the structure of Gyroid seems to be more complicated. A few months ago, when I mentioned our beaded models including the P- and D-type Schwarzites to Prof. Luh(陸駿逸), he suggested that we should try to construct gyroidal graphenoid, by which I mean a graphene embeded in a gyroidal surface. I didn't say too much at that time, since I knew only a little about this creature. Even now I still have only quite limited understanding about this surface form in particular, and IPMS in general. But this cannot prevent us to work on the construction of beaded structures of this type. Finally, Chuang has worked out how to tile graphene on a gyroid surface. The resulting gyroidal graphenoids look great on the screen of Chuang's PC. This is really remarkable. However to build a beaded model for the smallest system, we need about 120 beads per unit cell. To construct a 2x2x2 model, we need 1000 beads. The next smallest system, we need about 500 beads per unit cell. More than 4000 beads for a 2x2x2 model.
By the way, a good reference for people who are interested in the mathematics of shapes and their applications to chemistry is "The language of shape" by S. Hyde et al.
But the structure of Gyroid seems to be more complicated. A few months ago, when I mentioned our beaded models including the P- and D-type Schwarzites to Prof. Luh(陸駿逸), he suggested that we should try to construct gyroidal graphenoid, by which I mean a graphene embeded in a gyroidal surface. I didn't say too much at that time, since I knew only a little about this creature. Even now I still have only quite limited understanding about this surface form in particular, and IPMS in general. But this cannot prevent us to work on the construction of beaded structures of this type. Finally, Chuang has worked out how to tile graphene on a gyroid surface. The resulting gyroidal graphenoids look great on the screen of Chuang's PC. This is really remarkable. However to build a beaded model for the smallest system, we need about 120 beads per unit cell. To construct a 2x2x2 model, we need 1000 beads. The next smallest system, we need about 500 beads per unit cell. More than 4000 beads for a 2x2x2 model.
By the way, a good reference for people who are interested in the mathematics of shapes and their applications to chemistry is "The language of shape" by S. Hyde et al.
Friday, August 3, 2007
More thoughts on public arts
Prof. S.-F. Cheng told me that the public arts installed in our department have to be through a process of 公開招標, so it is not easy for our group to become qualified.
Yesterday, when I went to the men's room in the second floor of chem building, I noticed that there is a large empty bench right in front of toilet. It is not a bad idea to put some display there. Artwork made by beaded network can be a good choice. We can also ask for a competition for finding the best display to put on that bench in each Men's or Women's room. I suspect there are
benches somewhere in women's room.
In addition to beaded artworks, I will also be happy if I can put a bubble machine in, say, second floor's men's or women's room for people to enjoy the wonder of science even in the restroom. The kind of bubble machine I have in mind is basically a closed tank made of two large transparent glasses separated by about 10 cm. This is similar to a standard fish tank. The only difference is the depth of the tank is much thiner so that the soap film can form easily in between. Soap solution is in a special container at the bottom. Soap solution can then be blown into the tank to form beautiful foam once the fan is turned on by any people who want to play. Of course, the lighting on top of the device could play an important role.
Yesterday, when I went to the men's room in the second floor of chem building, I noticed that there is a large empty bench right in front of toilet. It is not a bad idea to put some display there. Artwork made by beaded network can be a good choice. We can also ask for a competition for finding the best display to put on that bench in each Men's or Women's room. I suspect there are
benches somewhere in women's room.
In addition to beaded artworks, I will also be happy if I can put a bubble machine in, say, second floor's men's or women's room for people to enjoy the wonder of science even in the restroom. The kind of bubble machine I have in mind is basically a closed tank made of two large transparent glasses separated by about 10 cm. This is similar to a standard fish tank. The only difference is the depth of the tank is much thiner so that the soap film can form easily in between. Soap solution is in a special container at the bottom. Soap solution can then be blown into the tank to form beautiful foam once the fan is turned on by any people who want to play. Of course, the lighting on top of the device could play an important role.
Triply Periodic Minimal Surfaces based on sp2 caron
Two problems we can ask:
1. Systematic tiling rules for P- and D-type Schwartizes. This problem probably has been solved by Chuang and Fan already. But I haven't seen their works yet.
2. Possibility of constructing other triply periodic minimal surfaces based on trivalent sp2 network. A quite complete list of triply periodic minimal surfaces can be found here:
triply periodic minimal surfaces
One can find more pages on minimal surfaces through google search.
1. Systematic tiling rules for P- and D-type Schwartizes. This problem probably has been solved by Chuang and Fan already. But I haven't seen their works yet.
2. Possibility of constructing other triply periodic minimal surfaces based on trivalent sp2 network. A quite complete list of triply periodic minimal surfaces can be found here:
triply periodic minimal surfaces
One can find more pages on minimal surfaces through google search.
P-Type carbon Schwartzite
These pictures show three different view angles for the same carbon Schwartzite with P-type minimal surface. This beautiful model contains eight unit cells. According to its creator, Chuang, the hardest part in the whole weaving process is the steric hindrance which may cause the difficulty of finding a feasible direction to put the thread through the bead.
Chuang also told me that in Lenosky's original paper on carbon Schwartzite, he pointed out that the two spaces partitioned by the carbon sheet are not identical due to the particular network structure required by trivalent carbon atoms. Indeed, we can easily see this from our beaded model. However, I wonder that if it is possible to find certain arrangement of carbon atoms such that these two spaces are identical. If not, can we prove it.
Subscribe to:
Posts (Atom)