I recently communicated with
Prof. Gillespie about the bead model of fullerenes. He raised a few questions on the way I interpreted the hard-sphere repulsion and its connection to the VSEPR (Valence shell electron pair repulsion) theory for AX
3 systems. (Even though, I am trying hard to convince him that this correspondence with suitable interpretation of beads. He still doesn't think bead model provides an example of VSEPR.) Through the discussion with him, I was inspired to look at the meaning of color beads more carefully.
In all of my previous bead models, I adopted a simple color scheme which is basically using a different color for each kind of nonhexagons. For a shared edge between a hexagon and a nonhexagon, we use nonhexagon's color for that shared edge.
However, we can also adopt a color scheme which has more chemical meaning simply by assigning one color to single bonds and another color to double bonds. From elementary chemistry, we know that each carbon atom has four valence electrons and should form four chemical bonds with its three neighbored carbon atoms in a fullerene. So we should also impose the following rules for arranging single and double bonds to satisfy the correct electron counting and molecular stability:
1. Surrounding each carbon atom, there are four electron pairs corresponding to two single bonds, and one double bonds, which can be represented by two white beads and one red bead, respectively.
2. Two connected double bonds (neighbored red beads) are strictly forbidden.
3. Three single bonds surrounding a central carbon atom will have an extra electron left without bonding and should correspond to a radical. This pattern is not energetically unfavorable and should be avoided either.
Each particular arrangement of single and double bonds correspond to the so-called valence bond (VB) structure. Usually, many VB structures can be found for a particular fullerene. A simple rule of thumb from quantum chemistry is that the more VB structures a fullerene has, the more stable the corresponding fullerene is. The ground state wave-function of the fullerene can be approximately expressed as a superposition of these VB structures.
Finding and enumerating all possible arrangements of single (white beads) and double bonds (red beads) in a fullerene with the above constraints is nontrivial.
As I have pointed out, the color pattern of C60 generated by the color scheme we used before corresponds to the most important VB structure of C60. Basically, in this VB structure, each of 12 pentagons consists of five single bonds and each of 20 hexagons consists of single and double bonds alternatively. One can in principle generate many more VB structures by rotating the single- and double-bond pattern in any of hexagons by one bond unit. This transformed hexagon is another Kekule structure of that hexagon.

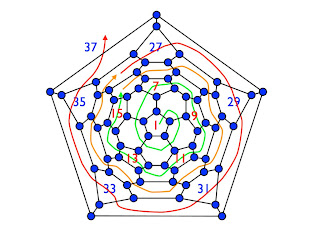
In addition to C60, I just constructed a bead model of C70 with a color pattern in consistent with one of its VB structures. It is not hard to see the beautiful labyrinth pattern for this particular color scheme. Although I don't have a proof, I suspect the generality for the existence of labyrinth pattern in the bead model (using this color scheme, of course) of any fullerene without free radical, i.e. carbon only with three single bonds (white beads in the following picture).
A particular VB structure (resonance form) of C70:
The corresponding bead model with a colored VB pattern: